Leap years
What is a leap year?
A leap year is a year that does not have 365 days like a normal year, but 366 days. The additional day ("leap day") is the 29th of February. A leap year occurs only every four years (for exceptions see below).
When is the next leap year?
The current year (2024) is a leap year. 2024 Calendar. The next leap year is 2028. The previous leap year was 2020.
Why are there leap years?
A tropical year (also called a solar year) is the time it takes for the earth to circle around the sun. This period is not exactly 365 days long, but 365.2422 days (365 days and a little less than 6 hours). By inserting a leap year, the calendar year is extended at regular intervals and thus synchronized with the tropical year. Without leap years, the calendar year and the seasons would slowly diverge.
Why is the 29th of February used as leap day?
In the Roman calendar, the month Februarius (which gave the name to today's month of February) was originally at 12th, and thus last, position at the end of the year, and was therefore the month to which a leap day was added (see Februarius and Julian Calendar on Wikipedia).
How are leap years calculated?
To align the tropical year of about 365.25 days in length with the 365-day calendar year, an extra day is added every four years. However, since the tropical year is slightly shorter than 365.25 days, a leap year is occasionally omitted. This is the case for years which are smoothly divisible by 100 (e.g., 1900 and 2100). However, there is an exception: years that are smoothly divisible by 400 (eg. 1600, 2000, and 2400) are leap years. Therefore three times in 400 years a leap year is omitted.
As a result of these adjustments, the average calendar year is 365.2425 days, so the deviations add up to just about one day in 3200 years.
On Wikipedia you will find further, very detailed information on the exact length of the tropical year and on the calculation of leap years.
For readers with interest and knowledge of programming here is the calculation of a leap year in pseudocode:
if year modulo* 400 is 0 then is a leap year
else if year modulo 100 is 0 then is not a leap year
else if year modulo 4 is 0 then is a leap year
else is not a leap year
(*modulo: remainder of the division n divided by m, e.g. 2000 modulo 400 = 0)
As a result of these adjustments, the average calendar year is 365.2425 days, so the deviations add up to just about one day in 3200 years.
On Wikipedia you will find further, very detailed information on the exact length of the tropical year and on the calculation of leap years.
For readers with interest and knowledge of programming here is the calculation of a leap year in pseudocode:
if year modulo* 400 is 0 then is a leap year
else if year modulo 100 is 0 then is not a leap year
else if year modulo 4 is 0 then is a leap year
else is not a leap year
(*modulo: remainder of the division n divided by m, e.g. 2000 modulo 400 = 0)
List of leap years from 1600 to 2400
|
1600 1604 1608 1612 1616 1620 1624 1628 1632 1636 1640 1644 1648 1652 1656 1660 1664 1668 1672 1676 1680 1684 1688 1692 1696 |
1704 1708 1712 1716 1720 1724 1728 1732 1736 1740 1744 1748 1752 1756 1760 1764 1768 1772 1776 1780 1784 1788 1792 1796 |
1804 1808 1812 1816 1820 1824 1828 1832 1836 1840 1844 1848 1852 1856 1860 1864 1868 1872 1876 1880 1884 1888 1892 1896 |
1904 1908 1912 1916 1920 1924 1928 1932 1936 1940 1944 1948 1952 1956 1960 1964 1968 1972 1976 1980 1984 1988 1992 1996 |
2000 2004 2008 2012 2016 2020 2024 2028 2032 2036 2040 2044 2048 2052 2056 2060 2064 2068 2072 2076 2080 2084 2088 2092 2096 |
2104 2108 2112 2116 2120 2124 2128 2132 2136 2140 2144 2148 2152 2156 2160 2164 2168 2172 2176 2180 2184 2188 2192 2196 |
2204 2208 2212 2216 2220 2224 2228 2232 2236 2240 2244 2248 2252 2256 2260 2264 2268 2272 2276 2280 2284 2288 2292 2296 |
2304 2308 2312 2316 2320 2324 2328 2332 2336 2340 2344 2348 2352 2356 2360 2364 2368 2372 2376 2380 2384 2388 2392 2396 |
2400 |
Annual shift of the summer solstice
The following graph illustrates the annual shift of the summer solstice between 1750 and 2250 due to the leap year adjustment every four years and the leap year rules for years divisible by 100 and 400 years. The X axis (at the bottom, horizontal) shows the year numbers, the Y axis (left side, vertical) shows the date of the summer solstice in June (20th to 23rd).
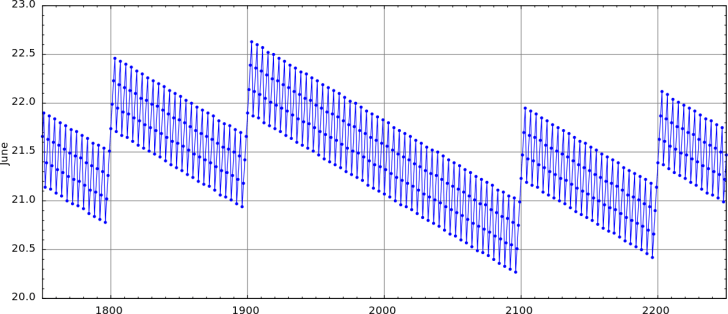
Annual shift of the summer solstice between 1750 and 2250 caused by the leap year adjustment every four years. Graph: Wikimedia creative commons
Additional information
On Wikipedia you'll find detailed information on leap years, the Gregorian calendar, which is the basis of our current calendar and which sets the rules for leap years as described above, and its predecessor, the Julian Calendar.
Calendar templates
Home · Sitemap / archive
Yearly calendars
Quarterly calendars
PDF · Word · Excel
Monthly calendars
Mar · Apr · May · Jun · Jul Weekly calendars
Daily calendars
PDF · Word · Excel
Hourly calendars
PDF · Word · Excel
Split year calendars 24/25
PDF · Word · Excel
School calendars 24/25
PDF · Word · Excel
Academic calendars 24/25
PDF · Word · Excel
Fiscal calendars 2024
PDF · Word · Excel
2 year calendars 24/25
PDF · Word · Excel
3 year calendars 24-26
PDF · Word · Excel
Photo calendars 2024
PDF · Word · Excel
Birthday calendars
PDF · Word · Excel
Blank calendars
PDF · Word · Excel
Perpetual calendars
PDF · Word · Excel
Yearly calendars
| PDF: | 2024 · 2025 / 2026 |
| Word: | 2024 · 2025 / 2026 |
| Excel: | 2024 · 2025 / 2026 |
PDF · Word · Excel
Monthly calendars
Mar · Apr · May · Jun · Jul Weekly calendars
| PDF: | 2024 · 2025 / 2023 |
| Word: | 2024 · 2025 / 2023 |
| Excel: | 2024 · 2025 / 2023 |
PDF · Word · Excel
Hourly calendars
PDF · Word · Excel
Split year calendars 24/25
PDF · Word · Excel
School calendars 24/25
PDF · Word · Excel
Academic calendars 24/25
PDF · Word · Excel
Fiscal calendars 2024
PDF · Word · Excel
2 year calendars 24/25
PDF · Word · Excel
3 year calendars 24-26
PDF · Word · Excel
Photo calendars 2024
PDF · Word · Excel
Birthday calendars
PDF · Word · Excel
Blank calendars
PDF · Word · Excel
Perpetual calendars
PDF · Word · Excel
Online Calendars
More...